-
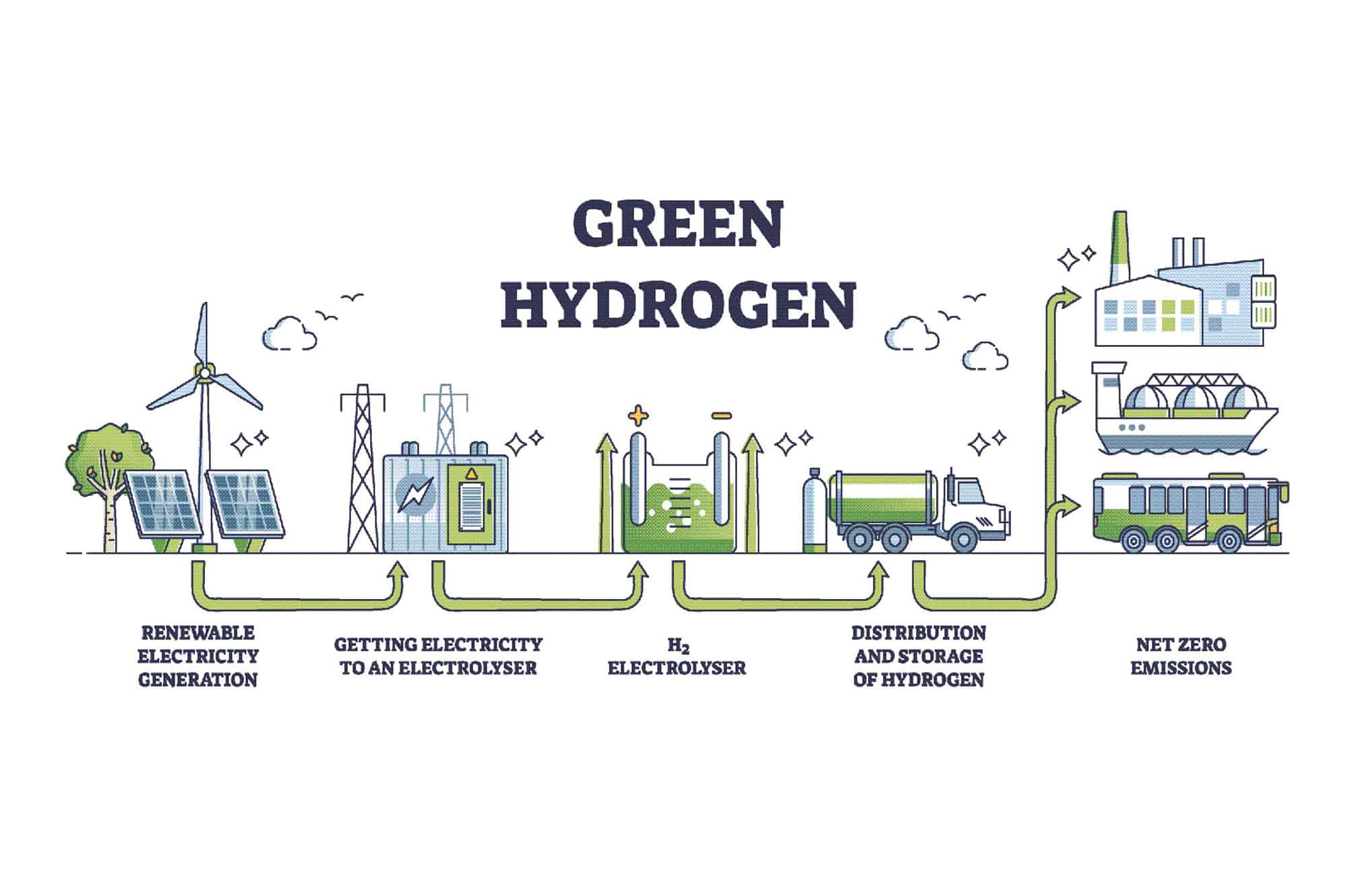
 ArticlesHydrogen: Push Towards the Generation of Green H2The desire to move to sustainable energy sources and reduce carbon emissions is growing exponentially. Low-cost renewable energy sources (e.g.,...
ArticlesHydrogen: Push Towards the Generation of Green H2The desire to move to sustainable energy sources and reduce carbon emissions is growing exponentially. Low-cost renewable energy sources (e.g.,... -
 ArticlesHydrogen Production: The Challenges and Practical ApplicationsAs the world shifts its focus to decarbonization initiatives, research shows responsible leaders will pour more technology and infrastructure into...
ArticlesHydrogen Production: The Challenges and Practical ApplicationsAs the world shifts its focus to decarbonization initiatives, research shows responsible leaders will pour more technology and infrastructure into... -
 ArticlesAn Aerospace Spin on Non-contacting Seal TechnologyNon-Contacting Sealing Technology Reduces Wear, Heat, Increases Life Expectancy Design features in the face of the mating ring force fluid (air,...
ArticlesAn Aerospace Spin on Non-contacting Seal TechnologyNon-Contacting Sealing Technology Reduces Wear, Heat, Increases Life Expectancy Design features in the face of the mating ring force fluid (air,... -
 ArticlesManufacturing in SpaceManufacturing in Space. It's a thing and there are several companies now working to figure out the complexities and solve...
ArticlesManufacturing in SpaceManufacturing in Space. It's a thing and there are several companies now working to figure out the complexities and solve... -
 ArticlesThe Mars Perseverance Rover’s Touch Down on the...With the world watching via live stream, the Perseverance Rover landed on Mars on Feb. 18, 2021. Technetics provides many...
ArticlesThe Mars Perseverance Rover’s Touch Down on the...With the world watching via live stream, the Perseverance Rover landed on Mars on Feb. 18, 2021. Technetics provides many... -
 ArticlesAerospace Sealing Solutions for Space MissionsCryogenic fluid management is the foundation for current and future space programs. The availability of these propulsive fluids at launch,...
ArticlesAerospace Sealing Solutions for Space MissionsCryogenic fluid management is the foundation for current and future space programs. The availability of these propulsive fluids at launch,... -
 ArticlesThe Benefits of High-Performance Metallic Seals in Critical...The unparalleled reliability of Technetics high-performance metallic seals excels in the face of numerous challenging scenarios.
ArticlesThe Benefits of High-Performance Metallic Seals in Critical...The unparalleled reliability of Technetics high-performance metallic seals excels in the face of numerous challenging scenarios. -
 ArticlesHow Technetics Excels in Semiconductor Innovation and PerformanceThe semiconductor market requires tremendous precision, and Technetics' engineered components that are up to the task.
ArticlesHow Technetics Excels in Semiconductor Innovation and PerformanceThe semiconductor market requires tremendous precision, and Technetics' engineered components that are up to the task. -
 ArticlesTechnetics Supports ITER; Reshaping Energy Production for the...ITER is a global collaboration working to forever change the way the world produces energy.
ArticlesTechnetics Supports ITER; Reshaping Energy Production for the...ITER is a global collaboration working to forever change the way the world produces energy. -
Articles & Information
We are continuously publishing thought leadership articles and insights to help our partners overcome critical challenges and uncover new, innovative solutions.
